1. What is Julia?
- Developed by MIT
- Fully open source
- Convenient syntax for building math constructs like vectors, matrices, etc
- Very fast
2. Getting Started
1. Run Julia in the cloud:
- JuliaBox
- Hassle free setup
- https://www.juliabox.org/
2. Run Julia locally (recommended):
- Faster and more flexible
- Requires some experience with command line
Install Julia:
Open the Julia application:
- You will be presented with a Julia command line
Create a Julia .jl file:
- Create and save a .jl file in a text editor
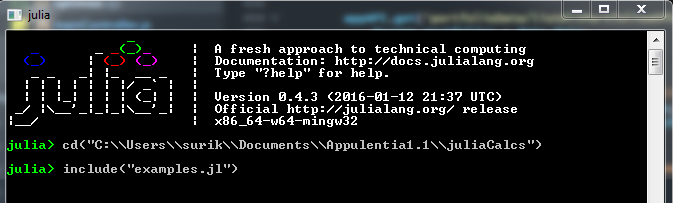
Open a Julia .jl file:
- cd to the directory where your .jl file is located – remember to use “ \\ ”
- Use “include” to run the .jl file
3. Basics
Types
- Integers: Int64, e.g. -45
- Real numbers: Float64, e.g. 1.256
- Booleans: Bool, true or false
- Strings: ASCIIString, e.g. “Hello World”
- Arrays: Array(Int64, 3) = 3 element array with Int64 values, e.g. [45, 3453, -23]
+, -, *, / Operators
Exponential’s
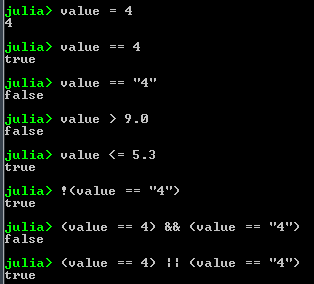
Boolean Expressions
- Evaluate to true or false
- Use the operators: == , != , < , > , <= , >=
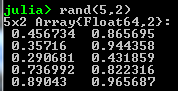
Random Numbers
- Generate a random number between 0 and 1
4. Variables
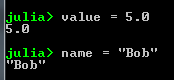
- Assignments use the = operator
- E.g. value = 5.0
- E.g. name = “Bob”
5. Control Flow (if statements, for loops)
If Else Statements
- We see the result when we run this file in Julia:
For Loops
- We see the result when we run this file in Julia:
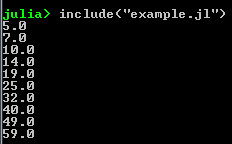
While Loops
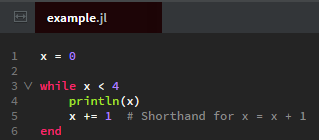
- We see the result when we run this file in Julia:
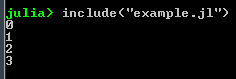
6. Functions
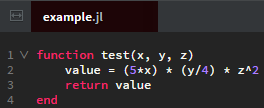
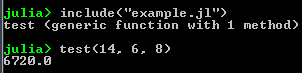
7. Arrays and Matrices
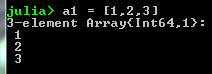
Arrays
- Arrays can be initialised directly:
- Or initialised empty:
- Arrays like this can be initialised with a type:
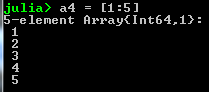
- Ranges can be used to create arrays:
- Arrays can also be generated from comprehensions:
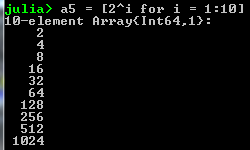
- We can access elements of the array:
- Arrays can be any type, so arrays of arrays can be created:
- We can push to arrays like so:
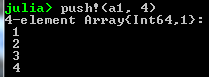
Matrices
- Matrices in Julia are represented by 2D arrays
- To create a 2×3 matrix:
- Semicolons delimit rows; spaces delimit entries in a row
- size(A) returns the size of A as a pair (n rows x m columns):
- Row vectors are 1xn matrices:
Indexing and Slicing
- Aij is found with A[ i, j ]:
- Ranges can also be used:
- : selects all elements along that dimension
- A[ : , 3 ] selects the third column:
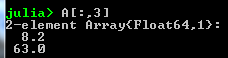
- A[ 2, : ] selects the second row:
- A[ : ] returns the columns of A stacked as a vector:
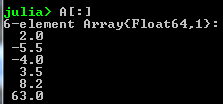
Common Matrices
- zeros( n, m ):
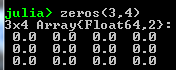
- ones( n, m ):
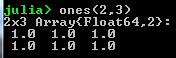
- eye(n):
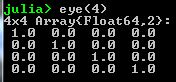
- diag(x) where x is a vector:
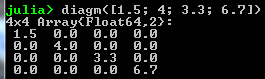
- Random nxm matrix:
Transpose and Matrix Addition
- A transposed is written “ A’ “:
- Adding and subtraction of matrices, e.g.
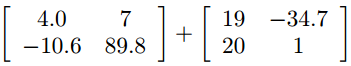
is written:
Matrix Scalar Operations
- All matrix scalar operations ( +, -, * ) apply element wise
- For e.g. matrix-scalar addition:
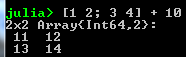
Is equivalent to:
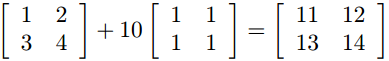
- Scalar multiplication:
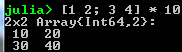
Is equivalent to:
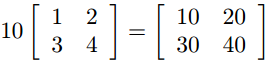
Matrix Vector Multiplication
- The * operator is used for matrix vector multiplication
- For e.g.
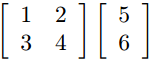
Is written:
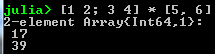
Matrix Multiplication
- The * operator is used for matrix multiplication
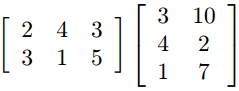Is written:
8. Packages
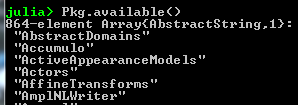
- List all available packages:
- Install one package (e.g. Calculus) and all it’s dependencies:
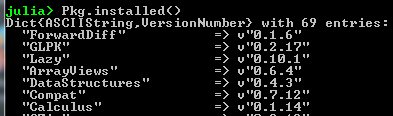
- To list all installed packages:
- To update all packages to their newest version:
- To use a package:
- This will import all functions of that package into the current namespace, so that it is possible to call:
- … without specifying the package it is included in
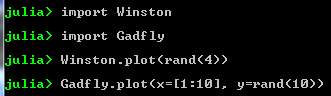
- You can also specify which package the function is called from:
- … using ‘import’ is especially useful if there are conflicts in function/type-names between packages
- For example, the plotting packages ‘Winston’ and ‘Gadfly’ both use the ‘plot’ function
- This can be prevented by using ‘import’, as follows:
